How Should Educators Interpret Value-Added Scores?

Stephen W. Raudenbush
and Marshall Jean
Highlights
- Each teacher, in principle, possesses one true value-added score each year, but we never see that “true” score. Instead, we see a single estimate within a range of plausible scores.
- The range of plausible value-added scores — the confidence interval — can overlap considerably for many teachers. Consequently, for many teachers we cannot readily distinguish between them with respect to their true value-added scores.
- Two conditions would enable us to achieve value-added estimates with high reliability: first, if teachers’ value-added measurements were more precise, and second, if teachers’ true value-added scores varied more dramatically than they do.
- Two kinds of errors of interpretation are possible when classifying teachers based on value-added: a) “false identifications” of teachers who are actually above a certain percentile but who are mistakenly classified as below it; and b) “false non-identifications” of teachers who are actually below a certain percentile but who are classified as above it. Falsely identifying teachers as being below a threshold poses risk to teachers, but failing to identify teachers who are truly ineffective poses risks to students.
- Districts can conduct a procedure to identify how uncertainty about true value-added scores contributes to potential errors of classification. First, specify the group of teachers you wish to identify. Then, specify the fraction of false identifications you are willing to tolerate. Finally, specify the likely correlation between value-added score this year and next year. In most real-world settings, the degree of uncertainty will lead to considerable rates of misclassification of teachers.
Introduction
A teacher’s value-added score is intended to convey how much that teacher has contributed to student learning in a particular subject in a particular year. Different school districts define and compute value-added scores in different ways. But all of them share the idea that teachers who are particularly successful will help their students make large learning gains, that these gains can be measured by students’ performance on achievement tests, and that the value-added score isolates the teacher’s contribution to these gains.
A variety of people may see value-added estimates, and each group may use them for different purposes. Teachers themselves may want to compare their scores with those of others and use them to improve their work. Administrators may use them to make decisions about teaching assignments, professional development, pay, or promotion. Parents, if they see the scores, may use them to request particular teachers for their children. And, finally, researchers may use the estimates for studies on improving instruction.
Using value-added scores in any of these ways can be controversial. Some people doubt the validity of the achievement tests on which the scores are based, some question the emphasis on test scores to begin with, and others challenge the very idea that student learning gains reflect how well teachers do their jobs.
Our purpose is not to settle these controversies, but, rather, to answer a more limited, but essential, question: How might educators reasonably interpret value-added scores? Social science has yet to come up with a perfect measure of teacher effectiveness, so anyone who makes decisions on the basis of value-added estimates will be doing so in the midst of uncertainty. Making choices in the face of doubt is hardly unusual – we routinely contend with projected weather forecasts, financial predictions, medical diagnoses, and election polls. But as in these other areas, in order to sensibly interpret value-added scores, it is important to do two things: understand the sources of uncertainty and quantify its extent. Our aim is to identify possible errors of interpretation, to consider how likely these errors are to arise, and to help educators assess how consequential they are for different decisions.
We’ll begin by asking how value-added scores are defined and computed. Next, we’ll consider two sources of error: statistical bias and statistical imprecision.[1]
What is a Value-Added Score?
Some districts define the value-added score as the average learning gain made by students on a standardized test in a given teacher’s classroom, in a specific subject area, in a specific year. More specifically, these districts test students annually and compute for each student the difference between the end-of-year test score and the test score that the student produced one year earlier. The average of these differences taken over all students in the classroom is defined as the teacher’s value-added score for that year.
The notion that “value-added equals average learning gain” has intuitive appeal. It seems reasonable to assume that a teacher is accountable for how much her students learn while attending her class. Measuring growth strikes many as far preferable to holding teachers accountable only for end-of-year test scores. After all, how much students know at the end of the year depends not only on what they learned that year, but on how much they knew when the year began. Because a teacher cannot influence how much the student knew at the beginning of the year, comparing end-of-year performance will work against teachers whose children began the year with less knowledge or skill. Comparing teachers by comparing learning gains seems to be a fairer reflection of their efforts.
Nevertheless, one might worry that a student’s test-score gain depends not only on how well the teacher teaches but on a number of other factors beyond a teacher’s control, including students’ family background and prior academic achievement. A simple classroom average gain could then be a statistically biased measure of teacher effectiveness, meaning it would systematically under- or over-estimate a teacher’s ability depending on the characteristics of the students assigned to her. To cope with this kind of bias, some districts have adopted a notion of value added based on more sophisticated statistical models. This approach starts with the idea of the average learning gain for the classroom, but it compares this average gain to the gain those students would be expected to achieve if they had been assigned to a teacher of average effectiveness. To do this, the model uses information about a student’s prior achievement, and sometimes information about his social and ethnic background, to predict how much he would gain if he were assigned to a typical teacher. The value-added score for a teacher, then, is the difference between the average actual gain of her students and their average expected gain. We will call this score “the adjusted average gain.”[2]
In sum, value added — defined as average gain or adjusted average gain — is intended to remove bias that would arise if we evaluated teachers based simply on students’ end-of-year test scores. But even a perfectly unbiased value-added score can be misinterpreted.
Errors of Interpretation
Errors of interpretation of value-added statistics have two sources: statistics may be biased, as described above, and they may be imprecise. The distinction between bias and imprecision is crucial. Imagine that a newborn child comes to a clinic to be weighed. Suppose that every nurse who weighs this child produces the identical weight: 7 pounds 4 ounces. The procedure by which the clinic weighs the infant is perfectly precise; estimates of weight have no variability. Suppose, however, that the scale that all the nurses used always produces an estimate that is 4 ounces over the true weight: the scale is upwardly biased. So the clinic produces a perfectly precise, but biased, estimate of child weight. Any comparison between that clinic and other clinics with respect to average birth weight would then be biased. In contrast, suppose that the individual nurses produce a variety of weights – say, from 6 pounds to 8 pounds. Suppose the average of these weights, 7 pounds, is correct. In this case, the procedure by which the clinic weighs infants is unbiased — the weights are correct on average — but highly imprecise: they vary randomly around the true weight. Any single estimated weight may be quite far off.
This brief will primarily consider how to interpret value-added statistics in light of imprecision. Fortunately, statisticians have proven techniques for quantifying the imprecision in problems like these, and using these techniques can guide justifiable interpretations of value-added scores, even in the face of uncertainty.
Informing the Teacher in Light of Imprecision
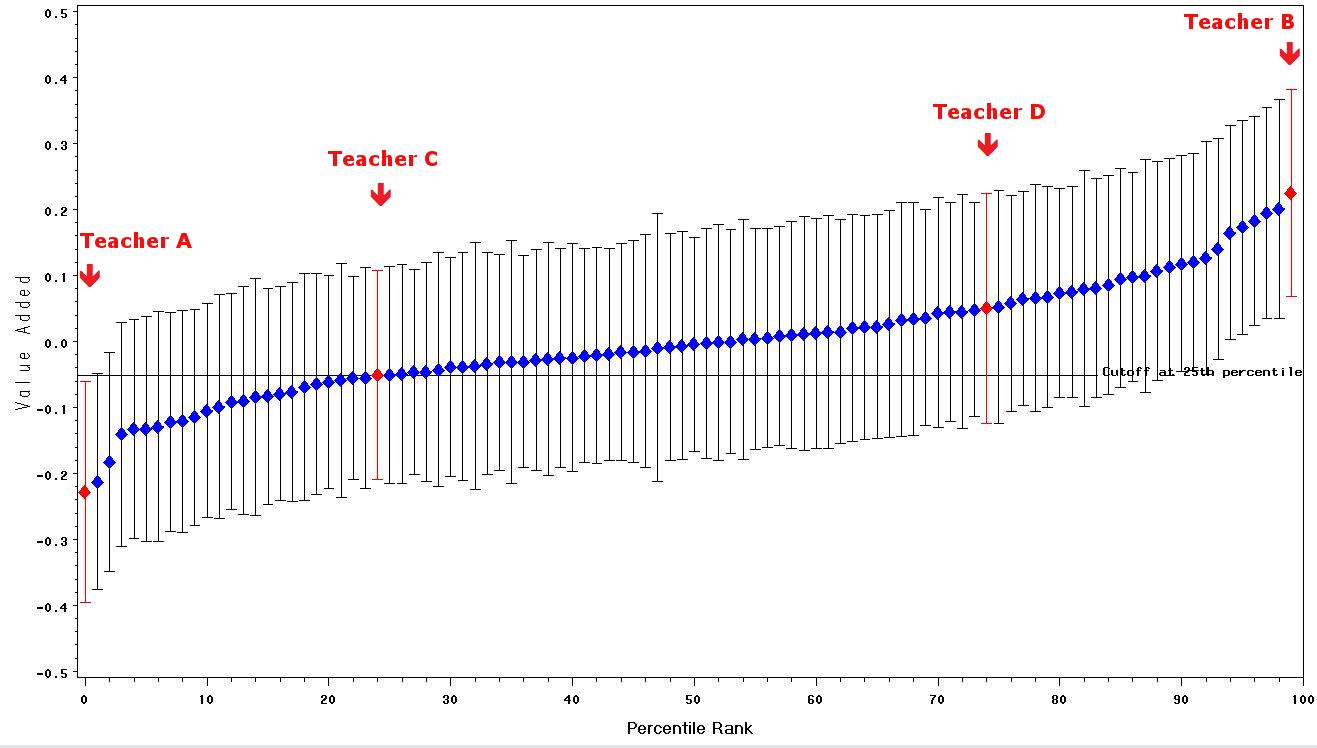
Let’s begin with a summary of evidence on value-added measurements that a teacher might actually see. Figure 1, sometimes called a “caterpillar plot,” displays scores for 100 teachers collected from an urban school district. The value-added score is on the vertical axis. On the horizontal axis we have the teacher’s percentile rank, from low to high as the axis goes from left to right; the teachers with the lowest value-added scores are at the left, and those with the highest are on the right, which is why the curve has an upward slope. What is notable about the graph is that, instead of associating a teacher with only a single number, the graph displays a range of plausible values.
The idea behind this display is that each teacher has produced a “true value-added score” but that the score we actually observe is an imprecise estimate of that score. The source of the imprecision is two-fold. First, the standardized tests used to construct the value-added statistics are not perfectly precise: the sample of test items used will vary from test to test, and the number of items is limited by the available testing time. So the test scores themselves are only approximations of what we would see if every student took an extremely long test. This means that the averages of student scores will contain some imprecision. Second, each teacher’s value-added score is computed from just one class of 20 to 30 students, a small sample of all the students that teacher might have in a given year or might be assigned in the future. Conceptually, we want value-added scores to generalize to those students the teacher might encounter rather than to the limited sample of students encountered in one year. So we define the “true value added” as being the average gain (or average adjusted gain) for this large universe of students. Although each teacher, in principle, possesses one true value-added score each year, we never see that true score. Instead, we see a single estimate within a range of plausible scores.
Confidence intervals
The range of plausible scores in Figure 1 is called a “95 percent confidence interval,” meaning that we have 95 percent confidence that the teacher’s true value-added score lies in the interval. The value in the middle of each teacher’s confidence interval is denoted by a diamond, and that is the value-added score for each teacher. Statisticians refer to this score in the diamond as a “point estimate,” because it is the single best estimate we have of the teacher’s true value added. But if the intervals are really long, the point estimate may not tell us much about the teacher’s true score. We see this same idea in reliable news accounts of election polls: we see a point estimate, e.g., “Candidate A leads candidate B by 6 points,” but also a margin of error, e.g., plus or minus 2 points.
Figure 1: Confidence intervals for the value-added scores for 100 teachers. The reliability of the value-added statistic is .48.
The confidence intervals help us make interpretations about the scores. Consider, for example, the teacher whose value-added statistic is the lowest in the data set (Teacher A) and the teacher with the highest score (Teacher B). Their point estimates differ by about .45 points, and it seems reasonable to conclude that Teacher B has produced a higher value-added score than did Teacher A. Intuitively, we draw this conclusion because the confidence intervals of the two teachers do not overlap. The highest plausible value of Teacher A’s value-added measurement is lower than the lowest plausible value of Teacher B’s.[3] We can also see that the highest plausible value added for Teacher A is below the 25th percentile (noted by the horizontal black line); the lowest plausible value for Teacher B is above that line.
In contrast, if we pick any two teachers nearer the middle of the distribution, we can see that, although their point estimates differ, their confidence intervals significantly overlap. Most of the plausible values for one teacher are similar to the plausible values of another. So we would be inclined not to place much emphasis on the difference between the two point estimates of two such teachers. Consider Teacher C (whose point estimate is at the 25th percentile of the distribution) and Teacher D (whose point estimate is at the 75th percentile). One might think that a teacher at the 75th percentile would have a much higher true value added than would a teacher at the 25th percentile. However, the 95 percent confidence intervals of these two teachers overlap considerably, so we cannot readily distinguish between them with respect to their true value-added scores.
Reliability
Many commentators have criticized value-added scores as being “unreliable.” How might we define “reliability”? Intuitively, we can reason that a plot of the type displayed in Figure 1 reflects a high level of reliability if many of the teachers have confidence intervals that do not overlap with those of many of the other teachers. In this case, we can reliably distinguish groups of teachers from each other.
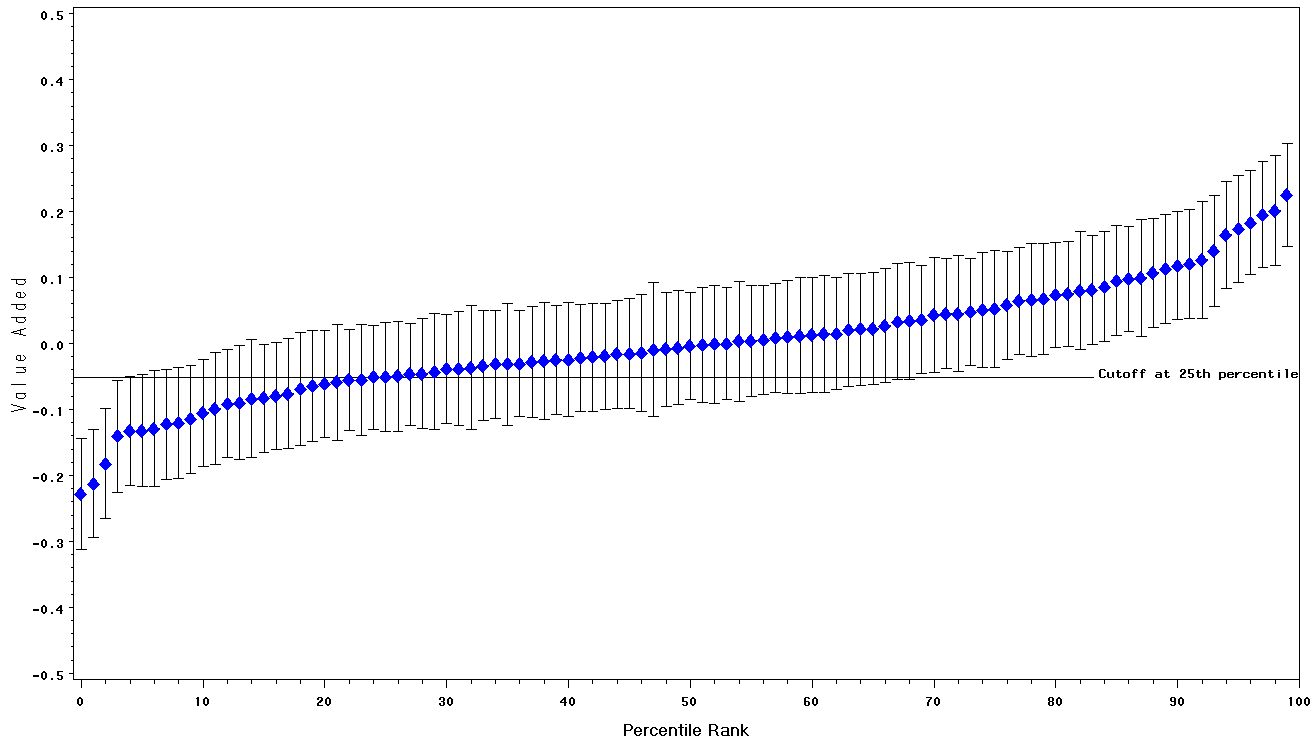
Two conditions enable us to achieve high reliability. First, if a teacher’s value-added measurement were more precise, the confidence intervals would be shorter, so there would be less overlap in comparing teachers at one part of the distribution with teachers at other parts, as displayed in Figure 2. This figure displays a caterpillar plot of the same type as that in Figure 1, but for a hypothetical sample of teachers in which measurement of value added is more precise.[4] Notice that in Figure 1, one finds it difficult to distinguish among the vast majority of teachers in the middle of the distribution. In contrast, Figure 2, with shorter confidence intervals, lets us distinguish between the lowest third of the teachers and the highest third. The confidence intervals are shorter because measurement of value added is more precise. This might happen if we tested students more than once a year, for example.
Figure 2: Confidence intervals for the hypothetical value-added scores for 100 teachers in a case in which the reliability of the value-added statistic is .67.
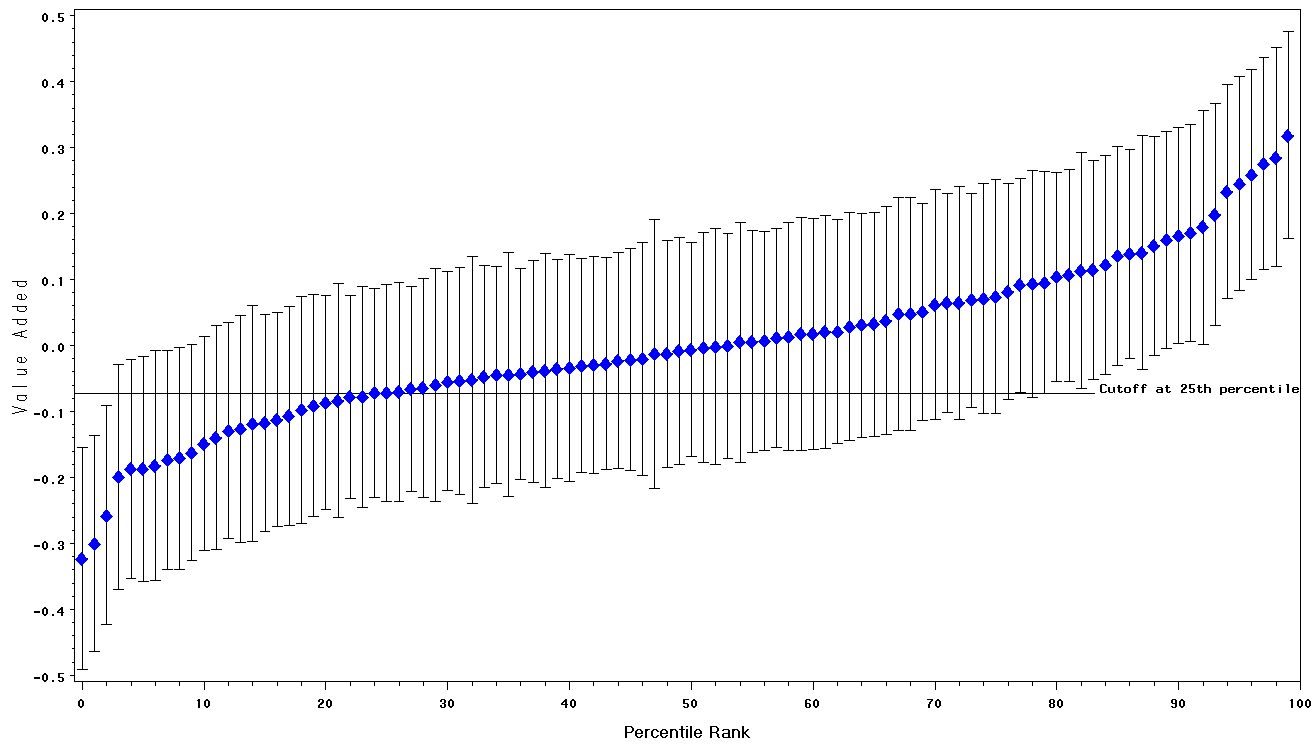
Second, if teachers’ true value-added scores varied more dramatically than they do, we could distinguish among them more readily — even if the precision of measurement remained unchanged. Figure 3 presents a hypothetical sample in which measurement precision remains unchanged, but teachers differ more in their true value added than do the teachers whose scores are displayed in Figure 1.[5] Thus, the slope of the curve described by the point estimates in the distribution in Figure 3 is steeper than the corresponding slope in Figure 1. We can now make many clearer distinctions among teachers simply because teachers are truly more variable.
Figure 3: Confidence intervals for the hypothetical value-added for 100 teachers in a case in which variance between observed value-added scores is higher. Reliability is .67.
Putting together these two insights, we can technically define the reliability of a teacher value-added statistic:
| (1) Reliability of VA = | Variation of “true scores”
Variation of “true scores” + Variation of measurement errors |
If teachers vary a lot in their true value added, the numerator of (1) will become large, thereby increasing the reliability (as in Figure 3). If the scores are highly precise, the measurement errors will be small (and therefore will have little variation); hence the denominator of (1) will diminish (as in Figure 2), and reliability will increase. The reliability of the value-added scores in Figure 1 is .48 while that in Figures 2 and 3 is .67.
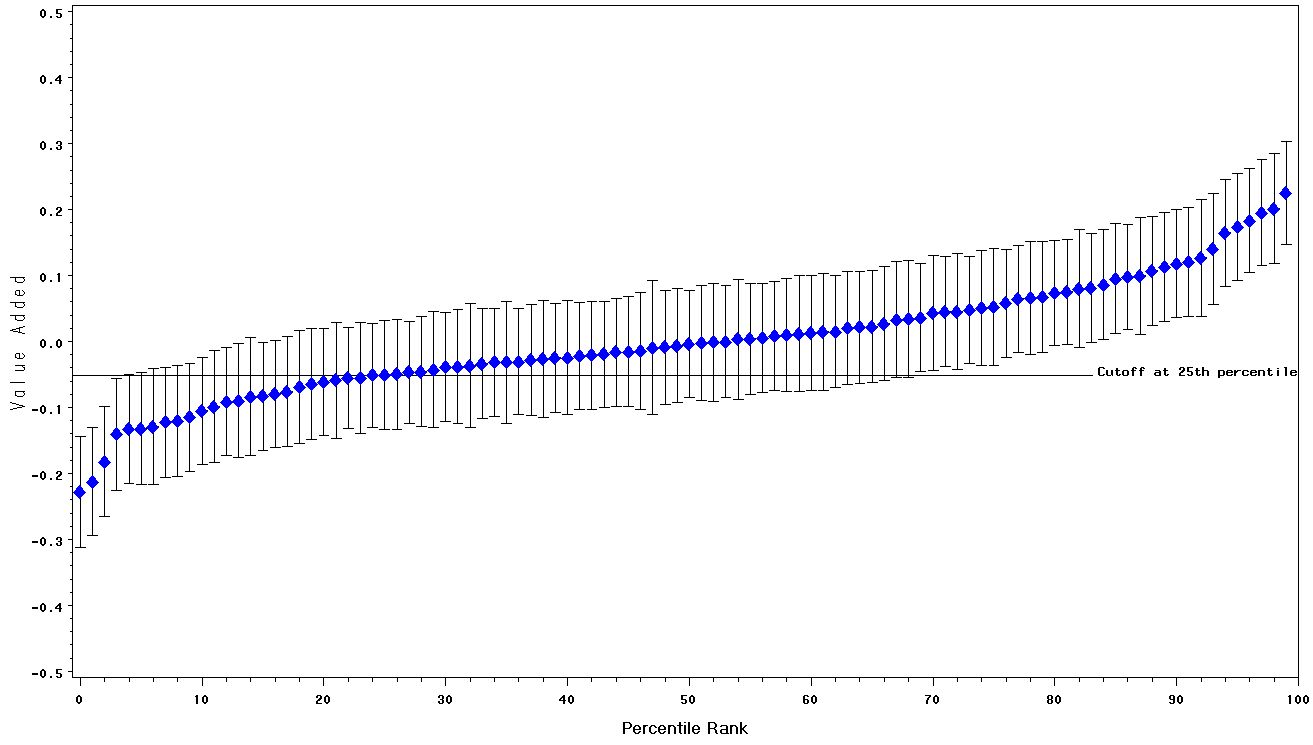
Degree of confidence. So far we have plotted 95 percent confidence intervals. We want 95 percent confidence that our interval captures the true value added. If we were willing to reduce our confidence level to, say, 75 percent, how would our confidence intervals change? We graph these 75 percent confidence intervals in Figure 4. Notice that the 75 percent confidence intervals in Figure 4 are centered on the same point estimates as are the 95 percent confidence intervals in Figure 1. However, the 75 percent intervals are shorter. We can therefore distinguish more easily among groups of teachers, but we do so with less confidence. In using such a figure for self-evaluation, a teacher might be willing to accept lower confidence about such comparisons.
Figure 4: 75 percent confidence intervals for the value-added scores for 100 teachers. The reliability of the value-added statistic is .48.
Classroom or teacher effects? Teachers do not create learning environments by themselves. Students may also act to improve or degrade the learning environment. In fact, one could argue that a particular teacher interacting with a particular group of students in a given year creates a unique learning environment with a unique chemistry that will not be perfectly duplicated in any future year. Many teachers report having “great” or not-so-great classes in a given year, and there is good empirical evidence supporting their view. Teachers’ performance can rise or fall for reasons ranging from personal events to changes of administration to actual gains in skill. Researchers who have calculated value-added scores in mathematics on multiple years for the same teacher show that the correlation in “true value added” is typically around .40 in mathematics. This means that about 16 percent of the variance in value added in any given year reflects comparatively stable differences between teachers, while the remainder represents unstable sources. Correlations would tend to be lower for subjects other than math.[6],[7] Thus, a caterpillar plot like Figure 1, which displays results for a single year, must be regarded as reflecting our conclusions about value added for a given class in a given year and not stable differences between teachers. It is possible and desirable to construct caterpillar plots like Figure 1 for a teacher’s average value added over two or more years. This would enable one to distinguish among teachers with respect to the stability of value added.[8]
The administrator’s view: Classification and decision-making in light of the imprecision of value-added estimates
While the teacher is likely to be most interested in where she stands in the distribution of value-added scores, an administrator may want to use this distribution to make decisions about certain groups of teachers. A superintendent might want to commend the teachers in the top 10th percentile; a director of instruction might want to identify teachers in the lowest 25 percentile for intensive professional development; and how teachers rank might influence decisions about promotion or pay. How, then, does our uncertainty about true value-added scores contribute to potential errors of classification? Glazerman and colleagues [9] developed a way of addressing this question. They reasoned as follows.
If value-added scores are measured with substantial error, a claim that a teacher lies, say, in the lowest 25 percentile of all teachers is also vulnerable to error. Two kinds of error are possible: a) “false identifications” of teachers who are actually above the 25th percentile but who are mistakenly classified as below it; and b) “false non-identifications” of teachers who are actually below the 25th percentile but who are classified as above it. These errors, of course, have very different consequences. Falsely identifying a teacher as below the 25th percentile may unfairly penalize that teacher, particularly if the scores were used for high-stakes purposes such as a salary freeze or termination. On the other hand, failing to identify truly ineffective teachers can hurt students, particularly if the ineffective teachers are given tenure. The less reliable the teacher value-added scores, the more frequent each kind of error will be.
Glazerman and colleagues developed a spreadsheet that works as follows: First, specify the group of teachers you wish to identify. In our illustrative example, we will hypothetically be trying to identify teachers“ needing improvement” whose true value-added scores are below the 25th percentile. Teachers above the 25th percentile will be proclaimed “satisfactory.” Second, specify the fraction of false identifications you are willing to tolerate. In our example, we tolerate 50 percent false identifications; that is, half of the teachers identified as needing improvement are actually satisfactory (above the 25th percentile). Third, specify the likely correlation between a value-added score collected this year and the value-added score a teacher is likely to generate next year. We assume a correlation of .40 based on the results of math value-added scores in the Measurement of Effective Teaching Project (2012) and consistent with the data in Figure 1. Once we have made these specifications, the spreadsheet will tell us what fraction of teachers we can actually identify.
If the correlation between this year’s and next year’s value-added measure were a perfect 1.0, we could identify the lowest 25 percent of teachers on the value-added statistics with no risk of error. Of course, that scenario is inconceivable: it would require the confidence intervals in Figure 1 to have zero length and teachers’ true value-added scores to be perfectly correlated from one year to the next. As the correlation gets lower, one must pick fewer than the bottom 25 percent of all teachers in order to avoid making excessive errors of classification.
To clarify just how this procedure works, consider Table 1, which displays the true and estimated value-added scores for a hypothetical sample of 1,000 teachers. We see from column (1) that of the 1,000 teachers, 250 are by definition below the 25th percentile in true value-added and therefore “needing improvement.” That means, of course, that the other 750 teachers are truly “satisfactory.” Based on a pre-post correlation of .40, the Glazerman calculations tell us we can identify 16 percent, or 160 teachers, as needing improvement (see Row 1), implying that 840 will be proclaimed satisfactory (Row 2).
As the table shows, we have correctly identified as needing improvement 80 teachers who are truly below the 25th percentile. We also see that we will have falsely identified as needing improvement 80 other teachers who actually are above the 25th percentile and therefore satisfactory. So, as anticipated, the false-identification rate is 50 percent. Notice, however, that we have also misidentified as satisfactory 170 teachers who, in truth, need improvement! Of the 250 teachers who actually need improvement, we failed to identify 170 — or 68 percent.
Decisions made under this level of uncertainty will strike many as completely unjustifiable. How can we tolerate a system that proclaims 160 teachers to be ineffective — that is wrong about these teachers half the time — and that fails to identify as ineffective more than half of the ineffective teachers? Advocates of value-added measures will argue that our current evaluation practices are even less accurate; we currently allocate teacher salaries based on years on the job and degrees obtained — criteria that have virtually no relationship to student learning.[10] This is equivalent to applying the Glazerman rules to the case in which the correlation between the predicted future value added and achievement is essentially zero. In this case, the administrator would not be justified in identifying any teachers as below the 25th percentile. And critics of the current practices of teacher evaluation say that is precisely what happens now: close to no teachers are identified as providing inadequate instruction under most evaluation systems.[11] Instead, teachers with low seniority are laid off, and teachers with high seniority stay on and earn raises.
Many supporters of value-added measures would avoid using these measures by themselves for high-stakes decisions. Instead, they advise using these scores to trigger further investigation; for example, they would conduct more intensive studies of the lowest-scoring teachers before taking any personnel action. This is a key argument made by many measurement experts: when confronted with uncertainty, seek more information.
Table 1:Table of correct and incorrect decisions if r=.40
| (1) Truly below 25th percentile | (2) Truly above 25th percentile | Total | |
| (1) Estimated to be below the 25h percentile | 80 (correctly identified as below the 25th) |
80 (falsely identified as below 25th percentile |
160 |
| (2) Estimated to be above the 25th percentile | 170 (falsely identified as above the 25th) |
670 (correctly identified as above the 25th) |
850 |
| Total | 250 | 750 | 1000 |
An argument for tolerating false identification of teachers is minimizing the risk to students. The 160 teachers identified as scoring below the threshold in Table 1 collectively will have substantially lower student achievement than will those not identified. Specifically, the Glazerman calculations suggest that the students of those 160 identified teachers will score about 1.00 standard deviation below the mean, while the students of the 840 teachers not identified will score about .16 standard deviations above the mean. The achievement gap of 1.16 standard deviations is large. So if identification of the 160 teachers leads to practices that boost student achievement (either through effective professional development or dismissal), students have a lot to gain. An important but unsettling conclusion from this kind of analysis is that reducing the risk of false identification for teachers heightens risks for students.
An important question regards the effectiveness of the 80 teachers hypothetically misclassified as below the threshold in Table 1. If those teachers are just slightly above the threshold on average, the claim that the system is unjust is undermined. However, if these misclassified teachers include a fair number of teachers who are actually very effective, the errors of misclassification may prove more severe than its proponents acknowledge. The Glazerman et al. calculations do not answer this important question. We used the data from Figure 1 to assess whether many highly effective teachers would be falsely identified as needing improvement in our hypothetical example. Specifically we computed 95 percent confidence intervals for the percentile rank of these lowest-scoring teachers. The upper bounds of these confidence intervals ranged from the 31st to the 74th percentile. Thus, it is implausible that a teacher in this group is truly in the top 25 percentile of true value added. It seems unlikely, then, that any of the best quarter of teachers, according to true value added, would be falsely identified as needing improvement. However, it is very likely that some of those teachers identified as needing improvement would be above the 50th percentile and therefore better than average in terms of true value added. It is important that any classification schemes based on value added consider the risk of falsely identifying very good teachers as ineffective. This concern does not yet seem to have arisen in the practical evaluation of value-added systems.
Practical Implications
How Does This Issue Impact District Decision-Making?
Imprecision is present in any personnel evaluation system. Standard statistical procedures help us cope with it. One rule is that we should examine confidence intervals rather than point estimates of teacher-specific value-added scores. On purely statistical grounds, it’s hard to justify publishing point estimates of teachers’ value added in local newspapers, especially without including any information regarding the margins of error. Even if the estimates are free of bias, the current level of imprecision renders such point estimates, and distinctions among them, misleading. A second rule is that administrators who want to use value-added statistics to make decisions about teachers must anticipate errors: falsely identifying teachers as being below a threshold poses risk to teachers, but failing to identify teachers who are truly ineffective poses risks to students. Knowing the reliability of the value-added statistics and, in particular, estimating their correlation with future gains in student learning, allows us to quantify the likelihood of making those errors under varied scenarios. These well-known techniques work when we assume that the measures of teachers’ value added are unbiased, and managing the problem of bias is important.